Interférences à N ondes de même amplitude, dont les phases forment une progression arithmétique.

On a pris ici N = 10 ; il faut bien réaliser que fréquemment (dans le cas d'un réseau par exemple), N est beaucoup plus élevé que cela. Mais avec un N beaucoup plus élevé, on n'aurait plus vu grand chose dans les animations ci-dessous... Il sera particulièrement intéressant, pour cette animation, de la télécharger pour pouvoir l'examiner image par image.
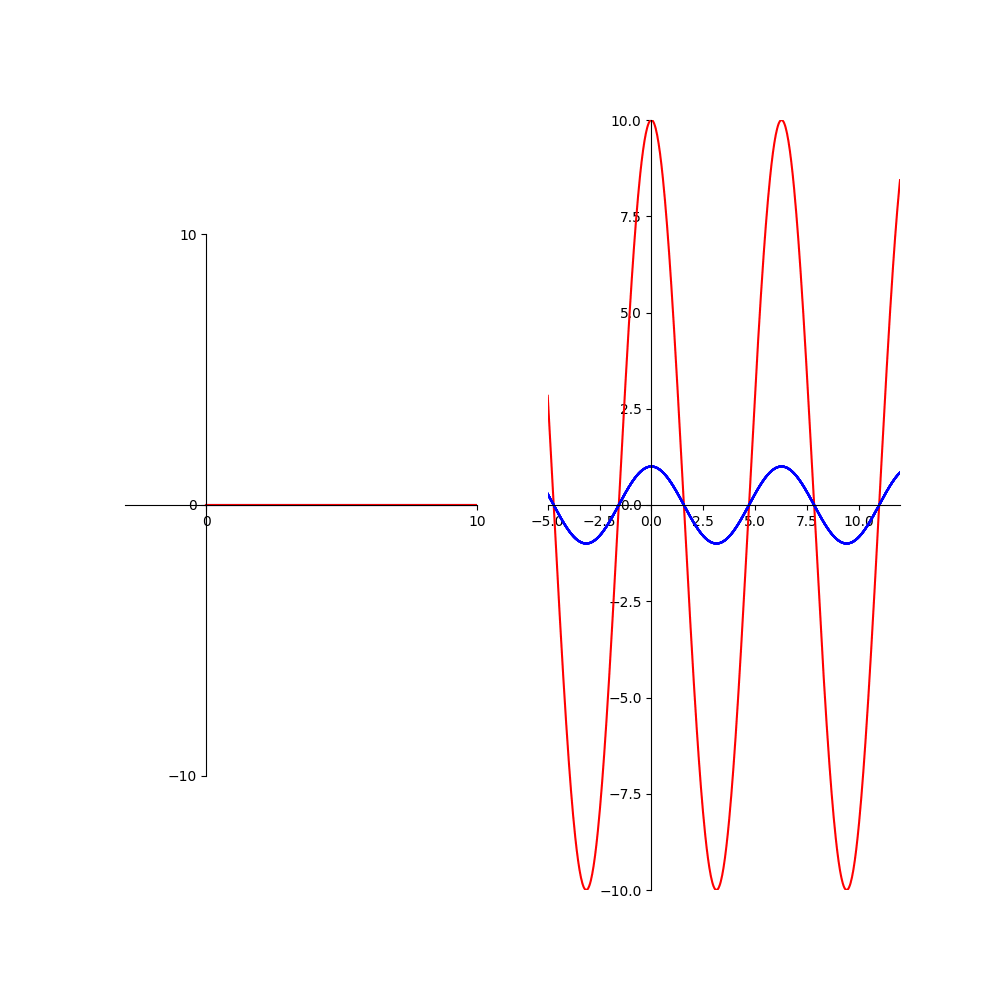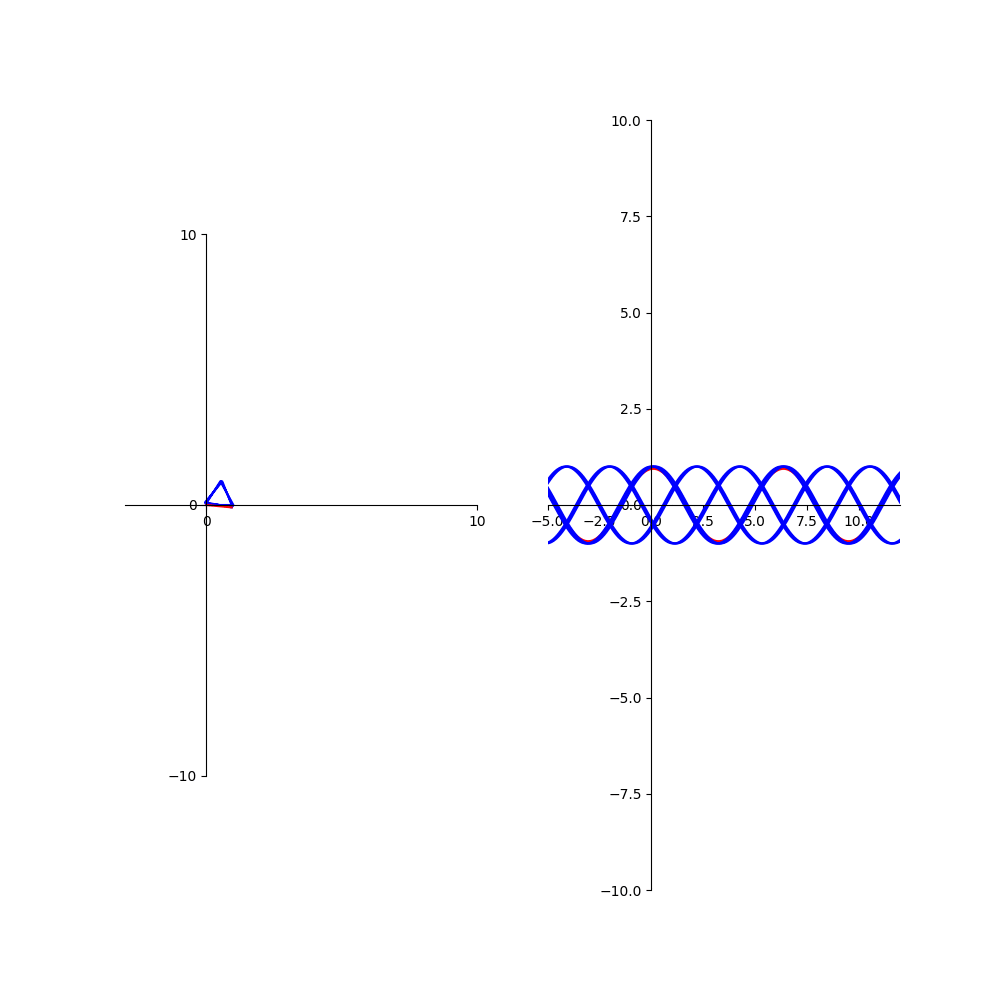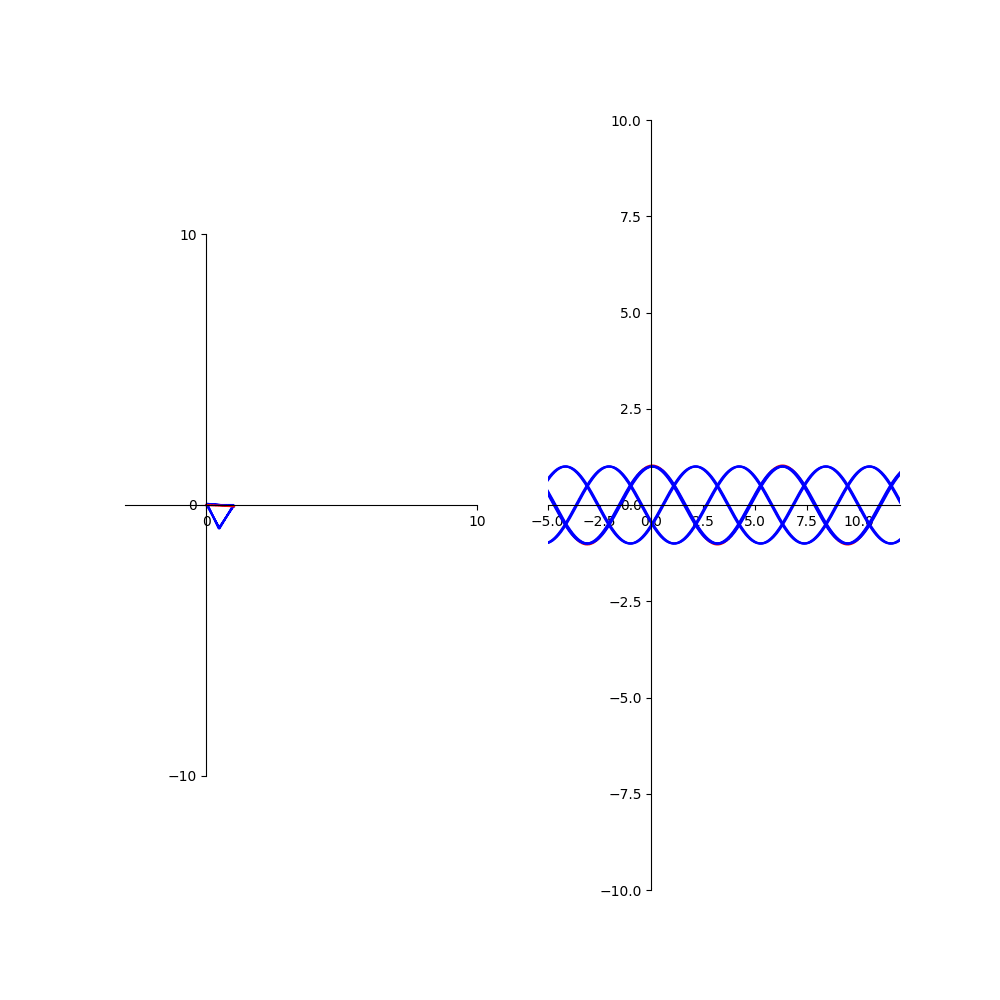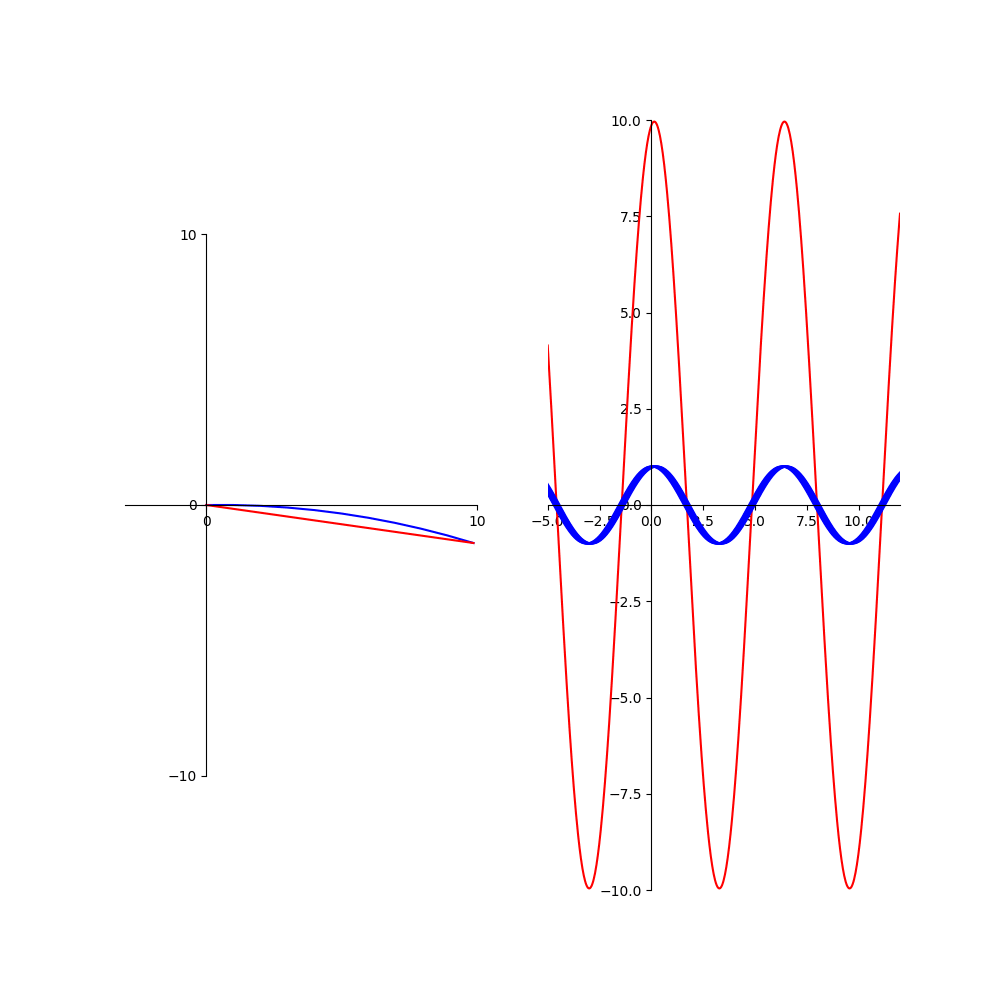
À gauche de la figure, se trouve la représentation de Fresnel de la superposition des N ondes : chacune des N ondes est représentée par un petit segment bleu. On voit bien que chaque onde est déphasée de la même quantité φ par rapport à la précédente. La somme des N ondes, elle, est représentée par le segment rouge. Attention : le paramètre de l'animation est ici le déphasage φ entre deux ondes successives, ce n'est pas le temps comme très souvent (d'une figure à la suivante, φ augmente un petit peu).
À droite de la figure, se trouve la représentation temporelle correspondante : l'abscisse est la date t. Figurent là aussi les N ondes, de même amplitude (prise arbitrairement égale à 1), et leur somme en rouge.
On rappelle que l'intensité observée est proportionnelle au carré de l'amplitude de la courbe rouge ; pour la plupart des valeurs de φ, on voit donc qu'elle vaut entre 0 et 1 environ, et qu'elle s'annule périodiquement. Par contre, lorsque φ est multiple de 2π, les N ondes bleues sont en phase et l'intensité vaut N^2.