Interféromètre de Michelson.
Il est à noter que les figures et animations qui figurent sur cette page sont des simulations.
Franges d'égale inclinaison.
Une figure de franges d'égale inclinaison (lorsque la différence de marche est très inférieure à la longueur de cohérence de la source) :
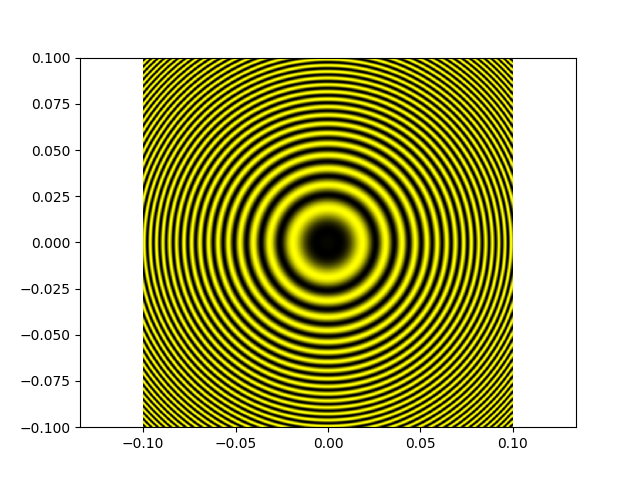
Maintenant on chariotte le miroir M2 (on notera que e augmente, puisque les anneaux sortent, et sont de plus en plus serrés) ; la différence de marche reste très
petite devant la longueur de cohérence de la source (et donc le contraste reste excellent) :
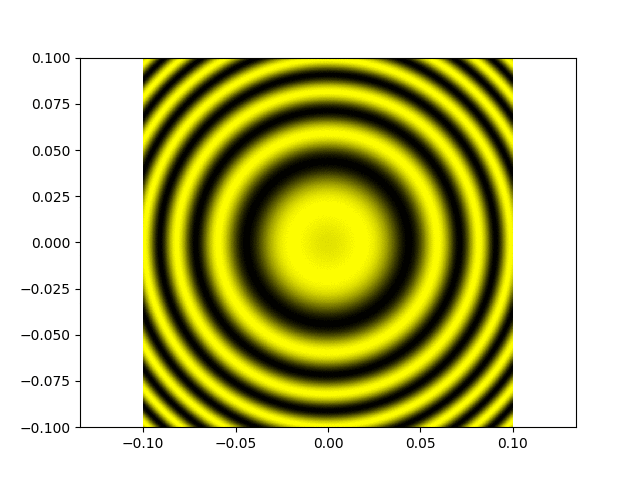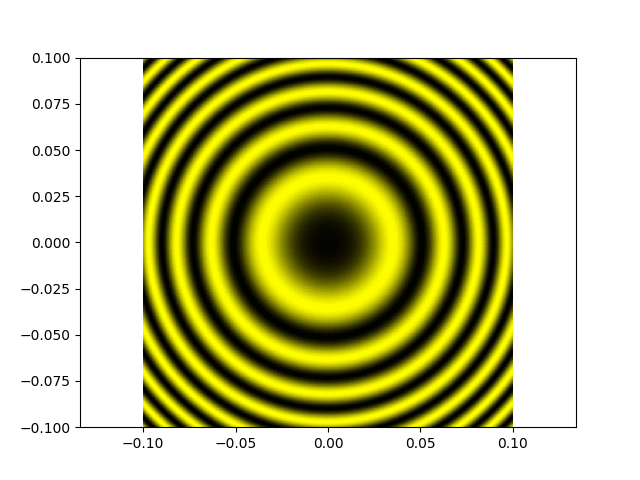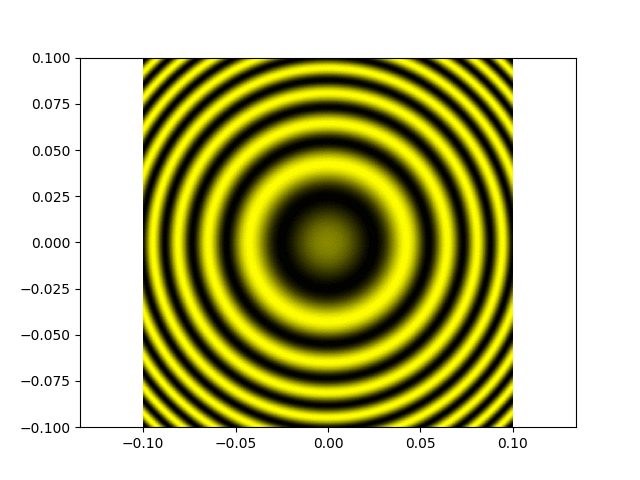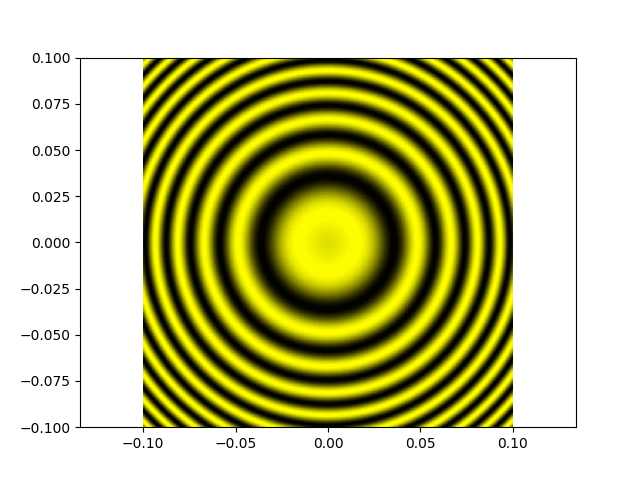
Même chose mais maintenant la différence de marche atteint la longueur de cohérence de la source, on voit le contraste diminuer graduellement, puis s'annuler (attention l'animation passe
"en boucle a priori donc après un certain temps elle revient au départ) :
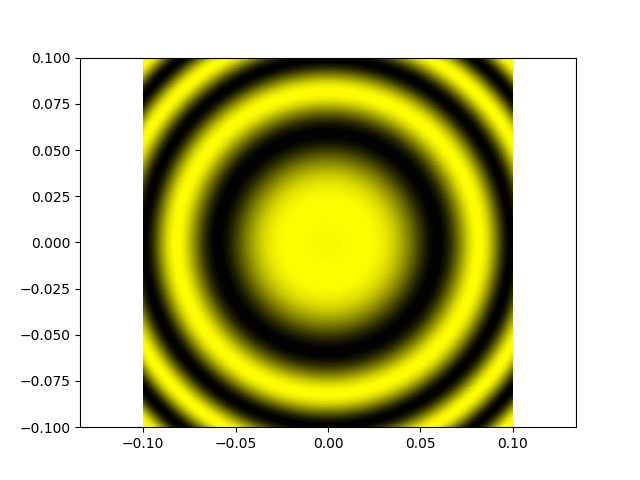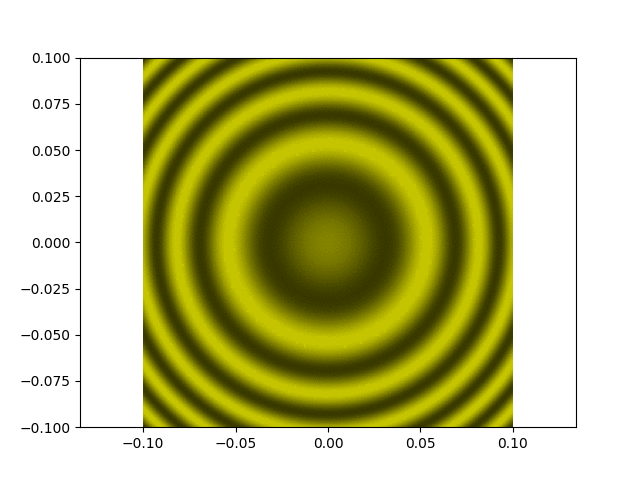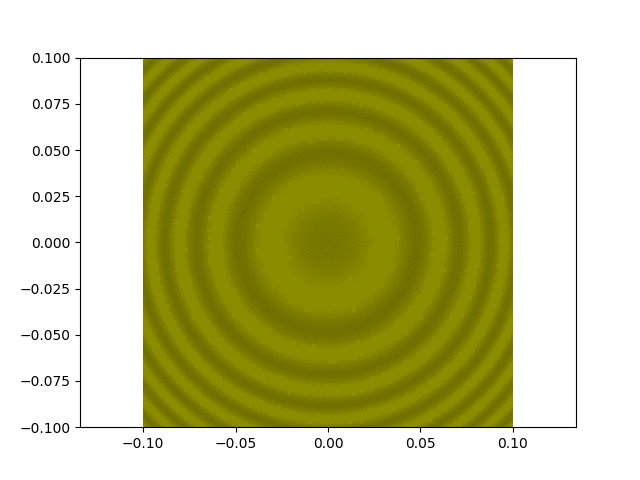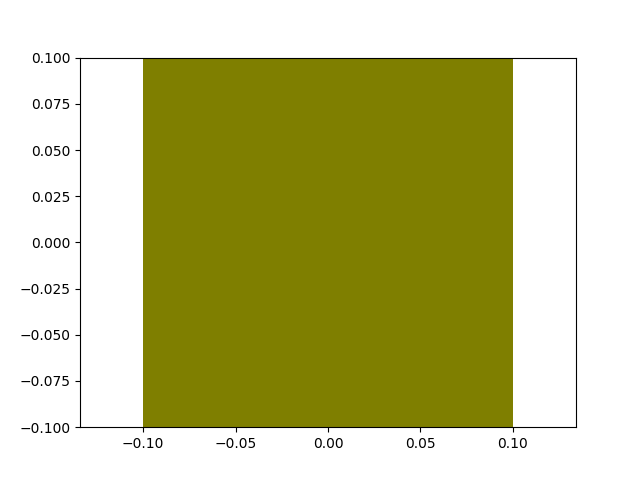
Ci-dessous la source est formée d'un doublet spectral : on observe que le contraste varie périodiquement entre 0 (brouillages car les
deux systèmes de franges sont en anticoïncidence) et 1. La simulation n'est pas parfaite, les franges évoluent un peu trop rapidement (et par ailleurs un effet stroboscopique
donne l'impression que les anneaux rentrent alors que e augmente), mais l'essentiel est de regarder l'évolution du contraste.

Et enfin dans le lien ci-dessous la source est une source de lumière blanche : on n'observe d'interférences qu'à proximité immédiate du contact optique. La différence de marche est alors
si petite qu'on ne peut pas voir d'anneaux, mais seulement une teinte uniforme sur tout l'écran. Dès que la différence de marche dépasse la longueur de cohérence
(très faible) de la source, on observe un écran blanc (mais il s'agit de blanc d'ordre supérieur).
Interféromètre de Michelson : teintes de Newton
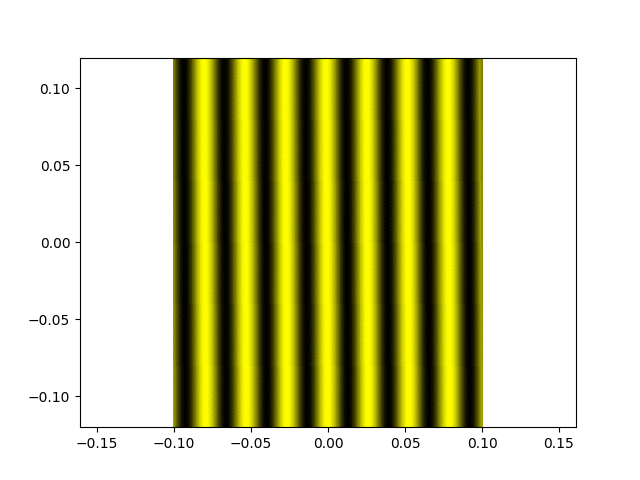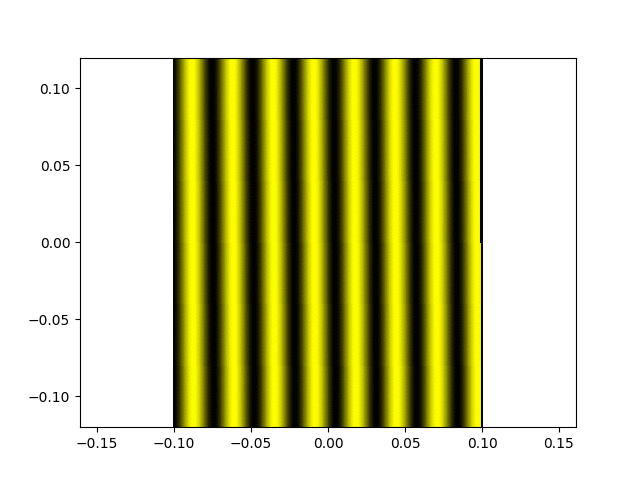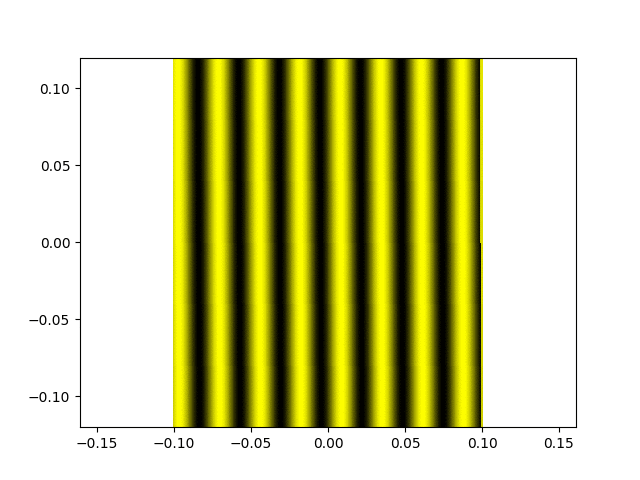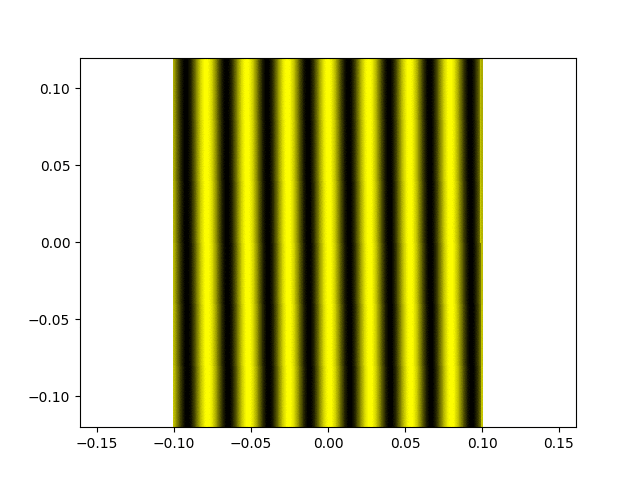
Franges d'égale épaisseur.
(section encore incomplète ; les effets d'une longueur de cohérence temporelle limitée n'ont pas encore été pris en compte)
Une figure de franges d'égale épaisseur (avec un bon contraste, donc la différence de marche est très inférieure à la longueur de cohérence de la source).
L'évolution de cette figure lorsque l'on chariotte.